Showing posts with label KS1. Show all posts
Showing posts with label KS1. Show all posts
Friday, 29 November 2019
History Key Questions To Ask When Learning About A Person, Event or Period in KS1
This blog post is now available at:
Labels:
curriculum,
curriculum development,
history,
KS1,
national curriculum
Monday, 18 June 2018
From The @TES Blog: Year 1 Should Be Like EYFS, Not Vice Versa
This piece that I wrote for the TES outlines a few questions that I have been asking myself about formalisation of teaching in the Early Years and in KS1 and beyond. It has met with a lot of praise from concerned Early Years practitioners and a certain amount of questioning from those more opposed to the ideas that I raise:
A key component of any phase of a child’s education is preparing them for the next stage, with an eventual goal of preparing them for the big wide world of work. Of course, this isn’t the only purpose of education – there are many immediate benefits, too. However, we try to ensure that Year 6 children are secondary-ready, we prepare our university-bound sixth formers for lectures and self-directed study and we want those leaving Reception to be "school-ready".
Click here to continue reading
Perhaps we need ask not how we can get children school ready, but how we can get school ready for the children?
Friday, 16 March 2018
From The @thirdspacetweets Blog: What Every KS2 Teacher And Maths Lead Needs To Know About NEW KS1 Maths Assessment Frameworks
Valentine’s Day 14th February 2018 brought KS1 teachers not one but two lovely treats: the teacher assessment frameworks for the 2017/18 academic year and the same document for the 2018/19 academic year.
While there are no changes for the current cohort of Year 2, the current Year 1s will be teacher-assessed on a new and amended framework.
Of course, the biggest question on everyone’s lips is…are the changes to the KS1 assessment framework for Maths an improvement?
To find out more, read on here: https://thirdspacelearning.com/blog/new-ks1-assessment-frameworks-maths-insights-ks2/
While there are no changes for the current cohort of Year 2, the current Year 1s will be teacher-assessed on a new and amended framework.
Of course, the biggest question on everyone’s lips is…are the changes to the KS1 assessment framework for Maths an improvement?
To find out more, read on here: https://thirdspacelearning.com/blog/new-ks1-assessment-frameworks-maths-insights-ks2/
Thursday, 14 December 2017
Scaffolding Structures for Reading Comprehension Skills
This is a very different blog post to the sort I normally write; it represents some very hypothetical thinking and the purpose of writing it is to open it up to discussion. My hypothesis is that the reading skills outlined in the English Reading Test Framework for KS2 (and KS1) might be best taught in a particular order. I also hypothesise that when teaching particular skills (represented as being higher up the model pictured) teachers can guide children through how to use other skills (lower down the model) to arrive at a better ability to practice and use the skills that are higher up the model. First of all, here's the model I've put together to which I refer:
Skills (taken from English Reading Test Framework for KS2)
are listed in the order that they might best be taught. This suggested order is
based on the idea that some reading skills might be required prior to
developing others. The most basic skills are towards the bottom.
The inclusion of 2d (inference) may depend on the text type.
For example, in many non-fiction texts there is no requirement to infer
information, only to retrieve it. In these cases the 2d (inference)
step/building block can be skipped.
The only reading skill from the test framework which isn’t
included here is 2h (make comparisons within the text). It is possible that
texts can be compared at many different levels, for example, the vocabulary
used can be compared (2a), summaries of plot can be compared (2c) or structure
of the text can be compared (2f). The skill of making comparisons (2h) could be
seen as a ‘floating’ skill – one which could be applied in different ways
alongside other reading skills.
All of the following symbols and colours refer to the Reading
Roles, a system I designed to make the different skills memorable for children
and teachers. Read more about the Reading Roles here: http://thatboycanteach.blogspot.co.uk/2016/12/reading-roles-cognitive-domains-made.html
2d – Inference (this
one is lots of detail here: http://thatboycanteach.blogspot.co.uk/2016/10/scaffolding-inference-trialling.html)
In order for children to begin to make inferences they need
to at least be able to retrieve information in the text, and before this they
need to be able to understand what the words mean.
(2a) give/explain the meaning of words in context
(2b) retrieve and record information/identify key details from
fiction and non-fiction
(2d) make
inferences from the text/explain and justify inferences with evidence from the
text
2f and 2g are very interlinked as they are both about
meaning – one with a focus on word and phrase choice, and one with a focus on
content choice. It is possible that 2g and 2f should precede 2d in the teaching
sequence but if making inferences is one way in which we take information from
a text, then arguably we need that information to make meaning; we can then go
on to identify and explain how that meaning is enhanced through word choice and
how the content included contributes to the meaning. The fact that these skills
are not included in the KS1 test framework might suggest that this is correct,
and that these are more advanced skills than making inferences.
2g – Author’s purpose
(2a) give/explain the meaning of words in context
(2b) retrieve and record information/identify key details from
fiction and non-fiction
(2d) make
inferences from the text/explain and justify inferences with evidence from the
text
(2g) identify/explain how meaning is enhanced through choice of
words and phrases
2f – Language
structure and choice
(2a) give/explain the meaning of words in context
(2b) retrieve and record information/identify key details from
fiction and non-fiction
(2d) make
inferences from the text/explain and justify inferences with evidence from the
text
(2g) identify/explain how meaning is enhanced through choice of
words and phrases
(2f) identify/explain how information/narrative content is related
and contributes to meaning as a whole
Once children understand word meanings, can find and infer
information, explain how language has been used to communicate meaning and, as
a result, can understand the meaning of a whole piece of text, then they can
begin to summarise the text, or make predictions based on their understanding.
It might not be necessary to summarise a text before making a prediction, and
the ability to summarise a text should not rely on the ability to make
predictions based on it. These two skills are both included in the KS1 test
framework, but children at this stage summarise and make predictions based only
on word meaning, information retrieval and inference (missing out 2f and 2g) –
summaries and predictions at this stage might be at a simpler level. It is
probably true that in KS2 similar summaries and predictions could be made,
without paying heed to 2g and 2f.
2c - Summarising
(2a) give/explain the meaning of words in context
(2b) retrieve and record information/identify key details from
fiction and non-fiction
(2d) make
inferences from the text/explain and justify inferences with evidence from the
text
(2g) identify/explain how meaning is enhanced through choice of
words and phrases
(2f) identify/explain how information/narrative content is related
and contributes to meaning as a whole
(2c) summarise main ideas from more than one paragraph
2e – Predicting
(2a) give/explain the meaning of words in context
(2b) retrieve and record information/identify key details from
fiction and non-fiction
(2d) make
inferences from the text/explain and justify inferences with evidence from the
text
(2g) identify/explain how meaning is enhanced through choice of
words and phrases
(2f) identify/explain how information/narrative content is related
and contributes to meaning as a whole
(2e) predict what might happen from details stated and implied
The model suggests that an understanding of word meaning is
core to all reading – this model assumes that children already have the skills
of decoding, sight recognition and phonological awareness. The model only
includes reading skills outlined by the test framework and does not include
factors such as the necessity of activating prior background and literacy
knowledge when reading.
The model also suggests that there is a hierarchy of reading
skills and that children might benefit from having some reading skills taught
before others.
It also suggests that when requiring a child to work on a
skill which is ‘higher up’ the model that they work through a sequence of
skills usage in order to initially scaffold their ability to exercise the
‘higher’ skill. For example, if requiring a child to summarise a passage, they
might first answer questions about the vocabulary used, the information
contained within (given both literally and inferentially) and what the authors
purpose was with regards to structure and language choices.
This model focuses on the following strands of Scarborough’s
reading rope: vocabulary, verbal reasoning and language structures:
I hope I have made my thinking clear in this blog post and I would really appreciate any thoughts about what I have proposed. If you can back any of your comments either with research or with case studies from experience then even better!
If you would like Aidan to work with you on developing reading at your school, please visit his website at https://www.aidansevers.com/services and get in touch via the contact details that can be found there.
Labels:
comprehension,
inference,
KS1,
ks1 sats,
KS2,
ks2 sats,
reading,
SATs,
scaffolding inference
Saturday, 2 December 2017
Mathematical Misconceptions And Teaching Tricks: What The Research Says
Imagine a factory. Think of the vast machines clanking away. Think of the whirring, the turning, the raw materials becoming a finished product. Beneath those metallic exteriors cogs, cams, belts and levers are working together to effect that change. But all but the most initiated don't really understand how the machines do what they do, they just know that if they put the right parts in at one end, the machine will produce the desired item.
And this is how many children feel about maths. They know that putting some numbers into a calculation will give the desired answer, but they don't really have a clue what goes on inside the 'machine' of that procedure. This is all well and good until that child has to apply this learning - having no understanding of the mechanics of mathematics makes it very difficult to use procedures in context.
In my blog post for Third Space Learning entitled 'Maths Tricks or Bad Habits? 5 Bad Habits in Maths We're Still Teaching Our Pupils' I make several suggestions for how to use visual representations to teach good conceptual understanding of some tricky aspects of the maths curriculum, such as the ones below:
If we don't do this, we run the risk of allowing children to proceed in their mathematical education with misconceptions:
In the bar modelling guide (click to download for free) I pointed out that:
By developing children's skills to represent and explain their understanding using a model, we develop their independence and motivation:
Further Reading and Resources:
And this is how many children feel about maths. They know that putting some numbers into a calculation will give the desired answer, but they don't really have a clue what goes on inside the 'machine' of that procedure. This is all well and good until that child has to apply this learning - having no understanding of the mechanics of mathematics makes it very difficult to use procedures in context.
In my blog post for Third Space Learning entitled 'Maths Tricks or Bad Habits? 5 Bad Habits in Maths We're Still Teaching Our Pupils' I make several suggestions for how to use visual representations to teach good conceptual understanding of some tricky aspects of the maths curriculum, such as the ones below:
The recent EEF guidance document on improving maths in KS2 and KS3 backs up the importance of modelling good conceptual understanding in maths lessons, rather than relying on tricks that work but don't help children to have an understanding of the 'why' and the 'how':
Recommendation 4: Enable pupils to develop a rich network of mathematical knowledge
"Pupils are able to apply procedures most effectively when they understand how the procedures work and in what circumstances they are useful. Fluent recall of a procedure is important, but teachers should ensure that appropriate time is spent on developing understanding. One reason for encouraging understanding is to enable pupils to reconstruct steps in a procedure that they may have forgotten. The recommendations in this guidance on visual representations, misconceptions, and setting problems in real-world contexts are useful here."In order to teach maths well, and in order for children to succeed in maths, teachers need to make sure children understand what is going on when they carry out a mathematical procedure. A great way of developing this understanding is using manipulatives and representations:
Recommendation 2: Use manipulatives and representations
"Manipulatives and representations can be powerful tools for supporting pupils to engage with mathematical ideas. However, manipulatives and representations are just tools: how they are used is important. They need to be used purposefully and appropriately in order to have an impact. Teachers should ensure that there is a clear rationale for using a particular manipulative or representation to teach a specific mathematical concept. The aim is to use manipulatives and representations to reveal mathematical structures and enable pupils to understand and use mathematics independently.
Teachers should: Enable pupils to understand the links between the manipulatives and the mathematical ideas they represent. This requires teachers to encourage pupils to link the materials (and the actions performed on or with them) to the mathematics of the situation, to appreciate the limitations of concrete materials, and to develop related mathematical images, representations and symbols."As I wrote in the guide to Bar Modelling that I produced for Third Space Learning (click to download for free):
If we don't do this, we run the risk of allowing children to proceed in their mathematical education with misconceptions:
Recommendation 1: Use assessment to build on pupils’ existing knowledge and understanding
"A misconception is an understanding that leads to a ‘systematic pattern of errors’. Often misconceptions are formed when knowledge has been applied outside of the context in which it is useful. For example, the ‘multiplication makes bigger, division makes smaller’ conception applies to positive, whole numbers greater than 1. However, when subsequent mathematical concepts appear (for example, numbers less than or equal to 1), this conception, extended beyond its useful context, becomes a misconception.
It is important that misconceptions are uncovered and addressed rather than side-stepped or ignored. Pupils will often defend their misconceptions, especially if they are based on sound, albeit limited, ideas. In this situation, teachers could think about how a misconception might have arisen and explore with pupils the ‘partial truth’ that it is built on and the circumstances where it no longer applies. Counterexamples can be effective in challenging pupils’ belief in a misconception. However, pupils may need time and teacher support to develop richer and more robust conceptions."When we do teach children using appropriate models and images so that they understand the mathematical concepts behind the procedures (or the 'tricks'), we provide children with something that they can actually look at and explain. Explaining something that is concrete is easier than explaining an abstract concept.
In the bar modelling guide (click to download for free) I pointed out that:
By developing children's skills to represent and explain their understanding using a model, we develop their independence and motivation:
Recommendation 5: Develop pupils’ independence and motivation
"Teachers can provide regular opportunities for pupils to develop independent metacognition through:Next time you plan a maths lesson question how you will ensure that children have a good conceptual understanding of the content you teach. Often, concrete or pictorial representations will be the best way to show children the inner-workings of the concepts you cover. Following Psychologist Jerome Bruner's research-based CPA (Concrete - Pictorial - Abstract) approach means that children (and adults) are more likely to understand what is going on inside the maths machine as calculations and processes take place.
- encouraging self-explanation—pupils explaining to themselves how they planned, monitored, and evaluated their completion of a task; and
- encouraging pupils to explain their metacognitive thinking to the teacher and other pupils."
Further Reading and Resources:
- These AET Mathematics plans give ideas for how to represent every single learning objective in the national curriculum from year 1 to year 11.
- My article for Third Space Learning: Maths Tricks or Bad Habits? 5 Bad Habits in Maths We're Still Teaching Our Pupils
- Articles by Mike Askew: KS1 and KS2 Maths – using visual models and Models in Mind
- Mr Bee's article: Fractions? I Love Fractions!
Monday, 25 September 2017
What Does 'Greater Depth' Look Like In Primary Maths?
This blog post is now available on my website:
Labels:
greater depth,
KS1,
KS2,
Maths,
national curriculum
Friday, 15 September 2017
9 Important Changes to the Primary Maths Curriculum and Assessment
In response to the DfE's latest documents, I wrote this for Third Space Learning. It's a summary of the key changes in the way primary maths will be assessed over the next few years:
On 14th September, just as we were all getting settled into the new school year, the DfE published not one, but two documents of considerable importance: ‘Primary assessment in England: Government consultation response’ and the 2017/2018 ‘Teacher assessment frameworks at the end of KS2’. Both documents reveal changes that will no doubt affect our approach as teachers and leaders.
Whilst the most imminent and significant changes involve writing and reading, there are also some interesting developments in Maths.
On 14th September, just as we were all getting settled into the new school year, the DfE published not one, but two documents of considerable importance: ‘Primary assessment in England: Government consultation response’ and the 2017/2018 ‘Teacher assessment frameworks at the end of KS2’. Both documents reveal changes that will no doubt affect our approach as teachers and leaders.
Whilst the most imminent and significant changes involve writing and reading, there are also some interesting developments in Maths.
Click here to read more: https://www.thirdspacelearning.com/blog/2017/9-changes-to-primary-maths-curriculum-and-assessment-slt-guide
The documents referred to throughout are these ones:
Primary Assessment Consultation Response: https://www.gov.uk/government/uploads/system/uploads/attachment_data/file/644871/Primary_assessment_consultation_response.pdf
Teacher Assessment Frameworks At The End of Key Stage 2: https://www.gov.uk/government/uploads/system/uploads/attachment_data/file/645021/2017_to_2018_teacher_assessment_frameworks_at_the_end_of_key_stage_2_PDFA.pdf
The documents referred to throughout are these ones:
Primary Assessment Consultation Response: https://www.gov.uk/government/uploads/system/uploads/attachment_data/file/644871/Primary_assessment_consultation_response.pdf
Teacher Assessment Frameworks At The End of Key Stage 2: https://www.gov.uk/government/uploads/system/uploads/attachment_data/file/645021/2017_to_2018_teacher_assessment_frameworks_at_the_end_of_key_stage_2_PDFA.pdf
Labels:
assessment,
DfE,
ELGs,
eyfs,
KS1,
ks2 sats,
Maths,
national curriculum,
SATs,
SATs ks2
Monday, 20 March 2017
On the TES Blog: Why Every Primary Should Be Using Bar Modelling – And Six Steps To Make It A Success
As a primary maths coordinator, it's been difficult to escape the lure of bar modelling: it's in every new publication, on all the maths blogs and at every coordinator's meeting. And so, when the time was right for my school, I succumbed.
Bar modelling, for the uninitiated, is not a method of calculation. Instead, it is a way of representing problems pictorially: from simple addition, through to finding percentages of amounts, all the way to complex multi-step problems involving ratio and proportion. Bar models can be used to pictorially represent arithmetic problems, as well as reasoning problems written with a context.
For a worked example of bar modelling and 6 steps to ensure introducing bar modelling is successful, read on at the TES blog:
https://www.tes.com/news/school-news/breaking-views/why-every-primary-should-be-using-bar-modelling
Bar modelling, for the uninitiated, is not a method of calculation. Instead, it is a way of representing problems pictorially: from simple addition, through to finding percentages of amounts, all the way to complex multi-step problems involving ratio and proportion. Bar models can be used to pictorially represent arithmetic problems, as well as reasoning problems written with a context.
For a worked example of bar modelling and 6 steps to ensure introducing bar modelling is successful, read on at the TES blog:
https://www.tes.com/news/school-news/breaking-views/why-every-primary-should-be-using-bar-modelling
Labels:
bar modelling,
KS1,
KS2,
mathematics,
Maths,
TES
Wednesday, 8 March 2017
Using Simple Bar Modelling Techniques To Solve Multi-Step SATs Problems
Bar Modelling is taking the primary maths world by storm. The 2014 curriculum appears, despite initial unhappiness, to be achieving a shift in the way maths is taught. Its three main aims of reasoning, problem solving and fluency have encouraged teachers to seek further ways to encourage conceptual understanding, rather than just teaching tricks or rules. So teachers have looked towards the countries who apparently churn out mastery-level mathematicians by the thousands for inspiration - that or some savvy publishers have decided to capitalise on the desire of teachers to teach the 'why' rather than the 'how'.
Click here to read more about bar modelling and the solution I came up with: https://thirdspacelearning.com/blog/2017/using-simple-bar-modelling-techniques-to-solve-multi-step-sats-problems
If you would like Aidan to work with you on developing maths at your school, please visit his website at https://www.aidansevers.com/services and get in touch via the contact details that can be found there.
Sunday, 29 January 2017
Why your Maths interventions for KS2 SATs should not start in Year 6
When a primary school receives good Key Stage 2 SATs results, the whole school celebrates, and rightly so: all teachers in all year groups will have contributed to the success of each child who reaches Year 6 and sits those tests.
However, it is not uncommon for Year 6 teachers to feel a pressure that teachers in other year groups don't. When results aren't so good it is more likely for the teaching and learning in that last year of primary, as opposed to any other, to be called into question - I know, I've been there myself. And with such pressure it's not surprising that in Year 6 we can descend into last-minute panic of revision classes, interventions and extra Maths and English time, often to the detriment of other areas of learning. Ideally this wouldn't happen.
Click here to read the rest of the article over at the Third Space Learning blog.
However, it is not uncommon for Year 6 teachers to feel a pressure that teachers in other year groups don't. When results aren't so good it is more likely for the teaching and learning in that last year of primary, as opposed to any other, to be called into question - I know, I've been there myself. And with such pressure it's not surprising that in Year 6 we can descend into last-minute panic of revision classes, interventions and extra Maths and English time, often to the detriment of other areas of learning. Ideally this wouldn't happen.
Click here to read the rest of the article over at the Third Space Learning blog.
Thursday, 1 December 2016
Reading Roles: Elements Of The Content Domain Made Memorable
This information can now be found at https://www.aidansevers.com/blog/search/reading%20roles
Labels:
cognitive domains,
KS1,
ks1 sats,
KS2,
ks2 sats,
ks2 testing,
reading,
reading roles,
SATs,
SATs ks2
Wednesday, 5 October 2016
Scaffolding Inference: Trialling a Teaching Technique
If you are short of time but would like to get the gist of this technique, please see my Quick Reference Guide: http://thatboycanteach.blogspot.co.uk/2016/11/scaffolding-inference-quick-reference.html

With inference being the most-assessed skill in the Key Stage 2 reading tests it is no wonder that teachers spend a lot of time attempting to teach children how to infer meaning from texts, with varying degrees of success. It's the sort of skill that readers (by that I mean those who make a regular habit of reading, and enjoy it) possess without really learning. Because of this, it is a skill that is hard to teach; many teachers infer naturally so deconstructing how they do it in order to teach a process to children can be difficult.

With inference being the most-assessed skill in the Key Stage 2 reading tests it is no wonder that teachers spend a lot of time attempting to teach children how to infer meaning from texts, with varying degrees of success. It's the sort of skill that readers (by that I mean those who make a regular habit of reading, and enjoy it) possess without really learning. Because of this, it is a skill that is hard to teach; many teachers infer naturally so deconstructing how they do it in order to teach a process to children can be difficult.
In case you missed it, the reading test framework has rearranged reading skills into eight content domains. The fourth domain, the one we are concerned with here, is:
2d: make inferences from the text / explain and justify inferences with evidence from the text
Background Reading
The chapter in 'Reading Reconsidered' entitled 'Writing for Reading' (read an excerpt here) discusses the various structures a teacher might use within a reading session. The ideas presented widen the scope of how different task sequences can support the development of different skills. This made me think more carefully about how the teaching and learning sequence could build to help children to infer more successfully.
The chapter in 'Reading Reconsidered' entitled 'Writing for Reading' (read an excerpt here) discusses the various structures a teacher might use within a reading session. The ideas presented widen the scope of how different task sequences can support the development of different skills. This made me think more carefully about how the teaching and learning sequence could build to help children to infer more successfully.
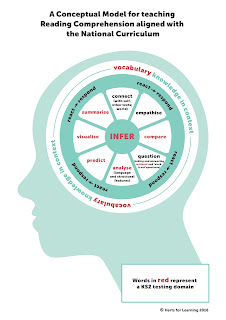
Penny Slater's helpful article 'Reading Re-envisaged' explores the links between vocabulary knowledge and inference skills initiated the thinking that led to my development and trial of this method. Her conceptual model (pictured left) represents how inference skills rely on good knowledge and understanding of vocabulary. In her own words:
"...the model signifies the importance of vocabulary knowledge. If we consider each circle to be a moat which the children must cross before they are able to access the skills within the innermost circles, then we see clearly that they will not get very far if they do not understand the meanings on the words on the page. This chimes with what teachers are finding in their classrooms: lack of knowledge of vocabulary is a complete blocker. You can’t make any inroads into comprehension without addressing this issue first."
Anne Kispal's 'Effective Teaching of Inference Skills for Reading', in section 2.3 (page 26) goes into more detail on this and the document as a whole is an informative read. It has also been shown that 95%-98% of the vocabulary in a text needs to be understood in order to be able to derive a general meaning of the text (Schmitt, Jiang & Grabe, 2011).
So, another content domain comes into play, one which children must be confident with if they are going to be able to make inferences:
So, another content domain comes into play, one which children must be confident with if they are going to be able to make inferences:
2a: give / explain the meaning of words in context
I also had an inkling that development of inference skills could be supported through the use of retrieval skills.
2b: retrieve and record information / identify key details from fiction and non-fiction
Children usually find retrieval easier than inference, however it is worth noting that in the 2016 KS2 tests even some of the retrieval questions were difficult, often because of the vocabulary skills that are needed in order to retrieve information. There are plenty of places to learn about how to improve vocabulary skills, so I won't go into detail on that in this article, but I must stress that it is important that children are taught skills such as contextual and morphemic analysis before they attempt the process I suggest. Before my own trial I spent around 4 weeks focusing on teaching vocabulary skills, allowing the children plenty of time to practice.
The Theory
The theory that I have been trialing is that inference skills can be taught by first studying the vocabulary used and then retrieving relevant information before going on to make inferences about a text. If inference is 'a conclusion reached on the basis of evidence and reasoning' then first a reader must be able to identify where the evidence is (retrieval) and before that the reader needs to understand the words used to present the evidence. In the model I propose (see right) the understanding of vocabulary is the foundation on which information retrieval is built, which in turn provides the support for making inferences.
The Practice
In short:
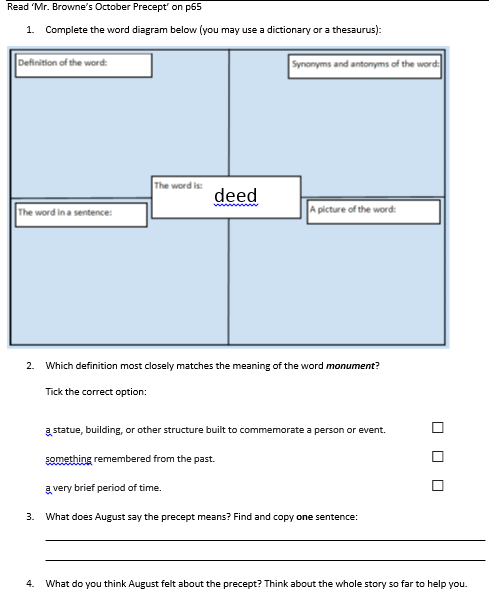
Here's an example of a very scaffolded set of questions - the scaffold questions (questions 1, 2 and 3) make the answer to question 4 very obvious.
This one worked so successfully that I actually encouraged the children to further their answers for number 4 by explaining how the evidence showed that the children were unsure how to treat August - this was not initially required of them, and when compared to similar questions in the 2016 KS2 test, this would be classed as an inference (2d) question without the addition of an explanation. It also made me contemplate giving them the inference question to answer before the scaffold questions, as well as after, in order to compare the difference and the impact the scaffold questions have on the quality of answer.
Some more activity examples:
One more example:
What Next?
If this way of scaffolding inference questions works for the children in my class then I will begin to adapt it in order to support the development of skills outlined in the other content domains:
The trial of this technique for scaffolding inference is in its infancy. As such I will follow up this blog post with others including commentary on what I learn, further examples of questions and some more examples of children's work showing the impact.
I would also love to engage in discussion on this idea - please use the comments section to tell me where I am going wrong, to point me in the direction of relevant research or additional reading or to share your own examples if you decide to try it!
Click here to read a testimonial from one teacher who used the technique.
Click here to read about how this, and other changes made to the way we teach reading, impacted on our SATs results.
The theory that I have been trialing is that inference skills can be taught by first studying the vocabulary used and then retrieving relevant information before going on to make inferences about a text. If inference is 'a conclusion reached on the basis of evidence and reasoning' then first a reader must be able to identify where the evidence is (retrieval) and before that the reader needs to understand the words used to present the evidence. In the model I propose (see right) the understanding of vocabulary is the foundation on which information retrieval is built, which in turn provides the support for making inferences.
The Practice
In short:
- Decide on an inference question (2d); the question stems based on the 2016 KS2 reading test made available by Herts for Learning on their blog are really useful for this.
- Begin to work backwards - work out where in the text the children need to go to locate useful evidence and ask a suitable retrieval question (2b).
- Continue to work backwards - which words or phrases do the children need to understand in order to be able to understand the evidence then ask a careful vocabulary question (2a).
- Once this process is complete (it may take a while at first), check that the 2a and 2b questions will adequately lead the children into answering the 2d question. If not, go back and tweak the questions.
There are different ways in which the 2a and 2b questions might provide a scaffold for answering the 2b question. In order to explain this I will share some examples. All the examples are based on 'Wonder' by R.J. Palacio. I chose 'Wonder' as our first class novel because although it is fairly heavy in subject matter, it is easy-going with its vocabulary. I wanted to begin by supporting children's acquisition of vocabulary skills in a non-threatening manner before we started to read novels with more advanced language.
The first excerpt takes place in the chapter entitled 'The Summer Table' in which a girl named Summer joins August who is alone at a lunch table on his first day at school.
In the first example (pictured above ) the scaffolding structure can be seen clearly: question 1 is a 2a question, question 2 is a 2b question and question 3 is a 2d question. There is a very obvious grammar discussion to be had to surrounding common nouns and proper nouns - the children asked for clarification on this despite the words in question 1 not being capitalised. The discussion we had cleared up possible later misconceptions that Summer meant the table was only for people named Summer - a misconception which would have been at odds with the basic fact that August was also sitting at the table. I've noticed that test questions are often set about texts with potential misconceptions so I try to take opportunities to incorporate similar tricky bits in my teaching.
The second example is taken from the same chapter; the text follows directly the previous excerpt:
The second example does not lead the children directly to the answer for question 3 but it does provide background knowledge which should inform their own thoughts on the motivation for Summer's actions. In answering question 1 the children realised that there was a long list of names and by answering question 2 they began to get the sense that the quote in question 3 was true; they gained their own insight into why August says that most of the names weren't actually summer names. Questions 1 and 2 allowed the children to understand what Summer was doing (making a long list, bending the rule that only children with summer names could sit on the table) before they began to think about why she was doing it.
Question 3 actually also requires previous knowledge of the text - the children must have already grasped that August (a boy with facial birth defects) is sitting alone on his first ever day in school whilst children whisper about his looks in order to infer that Summer agrees that so many children can sit with them so that he finds more friends. The more perceptive children might also realise that Summer also wants him to have fun so that he forgets about his situation and so that he feels like all the other children. I was satisfied that our previous reading and dialogic discussion (thanks Mat Tobin for the terminology) meant that they understood the whole text well enough to approach this question.
It should also be noted that here there are two retrieval questions and no vocabulary-based question; the vocabulary they needed had been covered in the previous set of questions.
Here is an example of a child's work. This task was undertaken independently directly after completing the previous task (see above). The first task was completed independently prior to a whole-class discussion and then children edited their answers (with a purple pen) based on the discussion that was had. This example contains no edits - the child was able to answer question 3 successfully first time. It is worth noting that this child is one of the best readers in my class - for her the scaffold has had almost immediate impact. In further blog posts on this subject I will provide before and after evidence.
Here is an example of a child's work. This task was undertaken independently directly after completing the previous task (see above). The first task was completed independently prior to a whole-class discussion and then children edited their answers (with a purple pen) based on the discussion that was had. This example contains no edits - the child was able to answer question 3 successfully first time. It is worth noting that this child is one of the best readers in my class - for her the scaffold has had almost immediate impact. In further blog posts on this subject I will provide before and after evidence.
For the next examples I must give credit to Rhoda Wilson for her excellent 'Moving Beyond Comprehension Sheets' resource as I used it along with the Herts for Learning question stems to vary the question styles in these activities.
Here's an example of a very scaffolded set of questions - the scaffold questions (questions 1, 2 and 3) make the answer to question 4 very obvious.
This one worked so successfully that I actually encouraged the children to further their answers for number 4 by explaining how the evidence showed that the children were unsure how to treat August - this was not initially required of them, and when compared to similar questions in the 2016 KS2 test, this would be classed as an inference (2d) question without the addition of an explanation. It also made me contemplate giving them the inference question to answer before the scaffold questions, as well as after, in order to compare the difference and the impact the scaffold questions have on the quality of answer.
Some more activity examples:
Here is an example of child's work. This child entered year 6 in September assessed at a year 4 standard for reading. This method appears to have been very successful for him, even after only a few times working in this way.
One more example:
What Next?
If this way of scaffolding inference questions works for the children in my class then I will begin to adapt it in order to support the development of skills outlined in the other content domains:
2c; summarise main ideas from more than one paragraph
2e: predict what might happen from details stated and implied
2f: identify / explain how information / narrative content is related and contributes to meaning as a whole
2g: identify / explain how meaning is enhanced through choice of words and phrases
2h: make comparisons within the textIt will also be important to begin to remove the scaffolding - for some children sooner than others - in order to encourage children to use the skills independently; one question often raised against methods such as this is how will this approach help children when the structure is removed, for example, in the SATs reading test? And it's a good question. My hope is that it will provide them with a method for answering inference questions; a method which will be embedded in their way of working. If this technique is successful then children will naturally make inferences using their ability to understand the vocabulary (these skills will need to be taught in addition to this method of scaffolding questions) and their ability to locate and retrieve information from the text.
The trial of this technique for scaffolding inference is in its infancy. As such I will follow up this blog post with others including commentary on what I learn, further examples of questions and some more examples of children's work showing the impact.
I would also love to engage in discussion on this idea - please use the comments section to tell me where I am going wrong, to point me in the direction of relevant research or additional reading or to share your own examples if you decide to try it!
Click here to read a testimonial from one teacher who used the technique.
Click here to read about how this, and other changes made to the way we teach reading, impacted on our SATs results.
Labels:
inference,
KS1,
KS2,
reading,
reading roles,
SATs,
scaffolding inference
Sunday, 21 February 2016
All Aboard!
In 'All In The Same Boat' I touched very briefly on today's subject matter and after a couple of conversations after yesterday's post it became clear that more needs to be said. Previously I wrote "Make sure your leadership are taking responsibility too - don't let them allow you to be alone in the boat" and I'd like to say a little more.
I am going to address this post to year 2 and year 6 teachers, but if you are a senior leader reading this, it is your responsibility to make sure that everything I suggest they do actually happens.
Most leaders will naturally want to be on board - it's their school and their data. Most leaders won't be leaving year 2 and year 6 teachers to hoist the mainsail themselves. Many leaders will now be adopting an 'all hands on deck' approach, but even the best captain needs to know from his crew what is happening in each area of the ship's life. He'll need the quartermaster to inform him when the ship is low on supplies, and he'll need the boatswain to tell him if such-and-such a part is in need of repair. Head teachers, and other members of SLT, will need feedback from teachers in order to understand what the needs and priorities are. And that's where this blog post comes in.
At the earliest possible opportunity, call a meeting with phase leaders (UKS2 and KS1), class teachers (Y2 and Y6), the head and any other SLT members. At the meeting discuss the new assessment arrangements (if you have not done so already) and its implications. If you have new thoughts and feelings after last week's revelations then it will be worth having another meeting anyway. It might be a good idea to take some assessment information with you so that you can identify the areas of greatest need. It'll also be good to approach it with some ideas already - if you go with only problems and no solutions the meeting will take longer, plus leaders always like to see a bit of initiative. Arm yourself with a list of questions you'd like to ask too. The meeting then needs to become a practical planning meeting with decisions made on what your school approach will be to this year's assessments. It's also worth considering as a team how you are going to keep a balanced curriculum instead of just doing maths and English (read this excellent blog post on the matter).
Even if you don't get to have a proper meeting, it'd be wise to ensure that the leadership of your school knows the course you are deciding to take with your year 2 or year 6 class. I would also involve them in any changes you're planning to make. Even when you begin to feel like you're pestering them, keep on asking for advice and informing them of your decisions.
The point of all this?
In short; make sure everyone is on board with everything that will end in assessment this year. Do everything you can do get the support that you need - even the best leaders need proactivity from their team.
Photo Credit: Eje Gustafsson via Compfight cc
I am going to address this post to year 2 and year 6 teachers, but if you are a senior leader reading this, it is your responsibility to make sure that everything I suggest they do actually happens.
Most leaders will naturally want to be on board - it's their school and their data. Most leaders won't be leaving year 2 and year 6 teachers to hoist the mainsail themselves. Many leaders will now be adopting an 'all hands on deck' approach, but even the best captain needs to know from his crew what is happening in each area of the ship's life. He'll need the quartermaster to inform him when the ship is low on supplies, and he'll need the boatswain to tell him if such-and-such a part is in need of repair. Head teachers, and other members of SLT, will need feedback from teachers in order to understand what the needs and priorities are. And that's where this blog post comes in.
At the earliest possible opportunity, call a meeting with phase leaders (UKS2 and KS1), class teachers (Y2 and Y6), the head and any other SLT members. At the meeting discuss the new assessment arrangements (if you have not done so already) and its implications. If you have new thoughts and feelings after last week's revelations then it will be worth having another meeting anyway. It might be a good idea to take some assessment information with you so that you can identify the areas of greatest need. It'll also be good to approach it with some ideas already - if you go with only problems and no solutions the meeting will take longer, plus leaders always like to see a bit of initiative. Arm yourself with a list of questions you'd like to ask too. The meeting then needs to become a practical planning meeting with decisions made on what your school approach will be to this year's assessments. It's also worth considering as a team how you are going to keep a balanced curriculum instead of just doing maths and English (read this excellent blog post on the matter).
Even if you don't get to have a proper meeting, it'd be wise to ensure that the leadership of your school knows the course you are deciding to take with your year 2 or year 6 class. I would also involve them in any changes you're planning to make. Even when you begin to feel like you're pestering them, keep on asking for advice and informing them of your decisions.
The point of all this?
- So that you're not alone in the boat at your school.
- So that you are supported.
- So that collective wisdom, and the wisdom that comes from experience, influences decisions.
- So that you have the chance to suggest that more manpower might be needed.
- So that when the data eventually comes in, it is data that represents a team effort.
- And so that no leader can make accusations of you, blaming poor results on you alone. This should not be about taking one for the team, but taking one AS a team.
In short; make sure everyone is on board with everything that will end in assessment this year. Do everything you can do get the support that you need - even the best leaders need proactivity from their team.
Photo Credit: Eje Gustafsson via Compfight cc
Saturday, 20 February 2016
All In The Same Boat

Now that we've all experienced the cocktail of initial relief, mild anger and nervous hilarity that the DfE's announcements yesterday generated, it's time to think soberly and wisely about it. My 'DfE Tells Teachers They're All Very Naughty' was a crude response, yet it did seem to voice the opinion and feeling of many teachers upon hearing what Mr. Gibb and Ms. Morgan had to say (@theprimaryhead's post was much better). What we teachers, however, really need to focus on now is making sure that, for our students, the next few months are worthwhile.
The positives that came out of yesterday's communication from the department are that it appears schools will not be judged too harshly based on the outcomes of this year's assessment. Nick Gibb wrote this in his letter to the NAHT:
"I have also written to Her Majesty’s Chief Inspector asking that his inspectors take into account national performance and the contextual factors you have outlined when considering a school's performance on writing at Key Stage 2. All organisations holding schools to account should be aware of the changes being introduced in 2016 and will consider the impact of this in making any decisions about performance or intervention on the basis of 2016 data alone. This should give schools the confidence to engage fully with the vision of the new curriculum and to rise to the new standards."
He's actually right. We should have the confidence to go on teaching, even if he had never said this. Even if we know our RAISE online could go blue next year. Even if we know Ofsted will not look kindly on us. Because what we have to focus on is the children - we have a responsibility to them first and foremost. And in a sense it has always been this way in year 6: teachers have always had the role of gatekeeper, protecting the children from the pressure. Sadly, some teachers have never managed this, instead subjecting children to weeks and weeks of practise papers under exam conditions and taking every opportunity to brow-beat them with "It's only x amount of weeks until your SATs, you know?" Some teachers pass on the pressure they feel - and, at all costs, we must not do that.
In another communication from yesterday the DfE let us know that:
"As this is the first year of new accountability measures and new assessments, we will wait until tests have been taken to set minimum expectations for a school’s progress scores."
We must also remember this: the scores will be calculated based on the tests taken nationally and if everyone does poorly then the minimum expectation will be set lower. We're all in this together and if the DfE stick to what they've said this week then perhaps we shouldn't worry as much.
Although the DfE have tried to shy away from admitting that this has all been a bit shambolic,lines like this give it away: "Significant reforms such as these take time to get right and for the system to catch up." We're all in the same boat; teachers, school leaders, inspectors and government officials should all be chalking this year up to experience.
At the end of my first year teaching in year 6 I thought my world was going to come crashing down around me. Some children hadn't achieved as highly as I had hoped, despite acing many a past paper. There were certain issues when comparing the data to the previous year's data. I thought I was for the chop. I spent hours writing documents to defend each and every poor test score, compiling evidence to prove that my teacher judgments weren't way off the mark. I sat in front of the school leaders and even our school improvement partner to defend myself. It all lasted about a week, and then life went on. They asked me to teach in year 6 again and my current school employed me to teach in year 6 too: last year saw a ten percent rise in children achieving floor standards or above.
That year when it all went wrong is now long gone and forgotten, in fact it was all gone and forgotten after a few weeks. The school went on to get a 'Good' Ofsted inspection (with two ares being 'Outstanding') despite the data which I thought would end the world (in fact, there was barely any mention of the data).
And when 2017 rolls around 2016 will be gone and forgotten too. Whatever happens this year will not be career-defining for you. Realising that every year 2 and 6 teacher in the land is in the same position is key to having a more positive outlook on this matter. Knowing that when schools are compared, aside from the usual variations, there will be a national trend. That trend will not necessarily be a trend of 'underachievement' because I know that every year 2 and 6 teacher in the country will be working their socks off to ensure excellent progress and high achievement for all their children. Possibly the tests, and even the teacher assessment based on the interim objectives, will show that we are 'underachieving', but we will all be there together - maybe then the DfE will admit that their handling of the changes was clumsy. Maybe they won't. Whatever happens, it will all blow over and we will all move on.
In the meantime, steel yourself for Monday, plan and teach some exciting lessons and make sure the kids are learning and making progress. Don't foist the stress on to them; they're just kids. Make sure your leadership are taking responsibility too - don't let them allow you to be alone in the boat. Do the wise thing and make sure you teach them according to the curriculum and the interim objectives - do what you can with the short time we've got, but just remember that there are only so many hours in a day, week, half term. Maximise that time so that you can be confident your children will 'perform' to the best of their ability. And that is all you can ask for.
Subscribe to:
Posts (Atom)